Структура ДАП

На рис. 10.1 приведена базовая конфигурация ДАП. Она выбрана таким образом, чтобы подчеркнуть сходство с сетями Хопфилда и предусмотреть увеличения количества слоев. На рис. 10.1 входной вектор

обрабатывается матрицей весов сети, в результате чего вырабатывается вектор выходных сигналов нейронов . Вектор затем обрабатывается транспонированной матрицей весов сети, которая вырабатывает новые выходные сигналы, представляющие собой новый входной вектор . Процесс повторяется до тех пор, пока сеть не достигнет стабильного состояния, в котором ни вектор , ни вектор не изменяются. Заметим, что нейроны в слоях 1 и 2 функционируют, как и в других парадигмах, вычисляя сумму взвешенных входов и вычисляя по ней значение функции активации . Этот процесс может быть выражен следующим образом:

или в векторной форме:

где

— вектор выходных сигналов нейронов слоя 2, — вектор выходных сигналов нейронов слоя 1, — матрица весов связей между слоями 1 и 2, — функция активации.

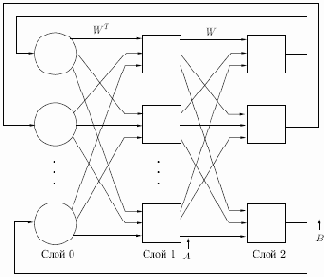
Рис. 10.1. 

Аналогично,

где

является транспозицией матрицы .

Как отмечено нами ранее, Гроссберг показал преимущества использования сигмоидальной (логистической) функции активации

где

— выход нейрона ,

— взвешенная сумма входных сигналов нейрона

, — константа, определяющая степень кривизны.

В простейших версиях ДАП значение константы

выбирается большим, в результате чего функция активации приближается к простой пороговой функции. В дальнейшем будем предполагать, что используется пороговая функция активации.

Примем также, что существует память внутри каждого нейрона в слоях 1 и 2 и что выходные сигналы нейронов изменяются одновременно с каждым тактом синхронизации, оставаясь постоянными в паузах между этими тактами. Таким образом, поведение нейронов может быть описано следующими правилами:

где

представляет собой величину выходного сигнала нейрона

в момент времени

.

Заметим, что, как и в описанных ранее сетях, слой 0 не производит вычислений и не имеет памяти; он является только средством распределения выходных сигналов слоя 2 к элементам матрицы

.

Содержание раздела

---